局部敏感哈希(LSH)与文本去重

本文旨在搞清楚哈希函数、局部敏感哈希、MinHash、SimHash之间的关系。对利用局部敏感哈希来做最近邻查找的问题做一个梳理和总结。本文主要参考stanford公开课cs246的课件，讲得非常清晰，要系统的理解一个问题，还是得看这种课件，比网上搜索的碎片化信息有用多了。课件链接在文末的参考文档中,文中的截图均来自课件。

目标问题

• 在高维空间里寻找相似的条目

  • 寻找相似的文章（查重）
  • 寻找相似的商品（电商推荐）
  • 寻找相似的图片 （以图搜图）

• 数学定义

  • 在高维空间的N个点X={x₁,x₂,…x,_n}中，寻找所有和目标点x 的距离d(x, x_i)小于给定阈值T的点。
  • 目标 O(N) -> O(1)

• 距离与相似度

  • 距离定义：
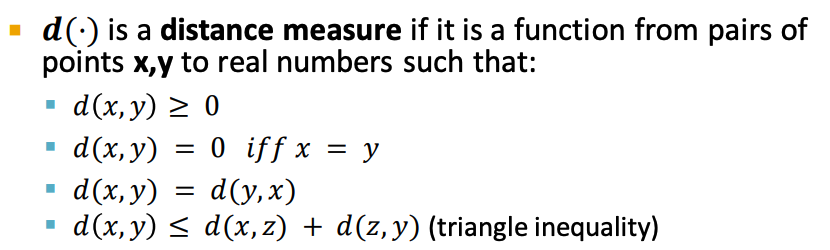
  • 例子:给定两个点 x=(0,1,2,3,4), y = (0,1,-2,0,4)
    • jaccard相似度: len({0,1,4})/len({0,1,2,3,4,-2}) = 3/6
    • jaccard距离： 1-jaccard相似度(从相似度定义衍生出来的距离，用来比较两个set。和维度的大小以及顺序无关)
    • cosine距离：arccos(x·y/|x|·|y|)/π
    • 欧氏距离： sqrt(0+0+16+9+0) = 5
    • 曼哈顿距离: 0+0+4+3+0 = 7
    • 汉明距离： 0+0+1+1+0 =2
  • 距离与相似度
    • 一般定义相似度=1-距离，但这两者有两个细微的区别
    • 相似度取值范围 [0,1], 距离可以定义在[0, inf]上
    • 距离函数需要满足三角不等式，相似度没有这个限制

总体思路

• 利用hash函数，将相似的点分配到同一个bucket(相等的hash值)。 然后对给定的点x，只需要在其对应的buket中比较。我们希望hash函数有如下两条性质，这样的hash函数被称为局部敏感哈希(LSH)

  1. 每个bucket中尽量含有少的点（减少False Positive，不相似的点尽量不要在同一个bucket中）
  2. 尽量减少False Negatives：（相近的点没有分在同一个bucket中，从而被遗漏掉）

• 形式化定义

  

• Hash 函数

  • 一系列函数，用来判断两个object是否相等
  • if x=y, hash(x) = hash(y)。 反之不一定
  • 不同应用场景下需要不一样的特性
    • hashmap：hash的结果尽量在值域上均匀分布，减少hash冲突
    • MD5等加密场景：减少冲突的同时不可逆计算
    • 局部敏感hash：原数据相近，大概率hash值相同

查重实战

给定一篇文章，在海量候选文章中找到与其相近的文章。（相近的定义取决于编码方式以及距离函数的选择）。主要分为一下三步

1. shingling:将文章编码成高维向量
2. min-hasing:利用LSH计算文章的哈希值
3. 优化S-Curve

shingling

• k-shingle(n-gram)切分
• 
• n越大，编码维度越高
• 可以用jaccard相似度定义文档相似度, 例如
  • A=abcabdd, B=abdadd, k=2
  • A={ab, bc, ca, bd, dd}, B= {ab, bd, da, ad, dd}
  • Sim(A,B) = len({ab, bd, dd})/len({ab, bc, ca, bd, dd, da, ad}) = 3/7
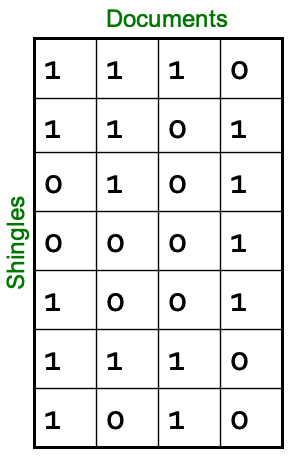
• N个文档可以转化为一个N列M行(M为所有文档的shingles的并集大小)的矩阵（非常稀疏）
• 如下图，4片文档，7个不同的shingles。1表示该文档包含该shingle，0表示不包含
  

  min-hashing

• min-hash是一种局部敏感hash
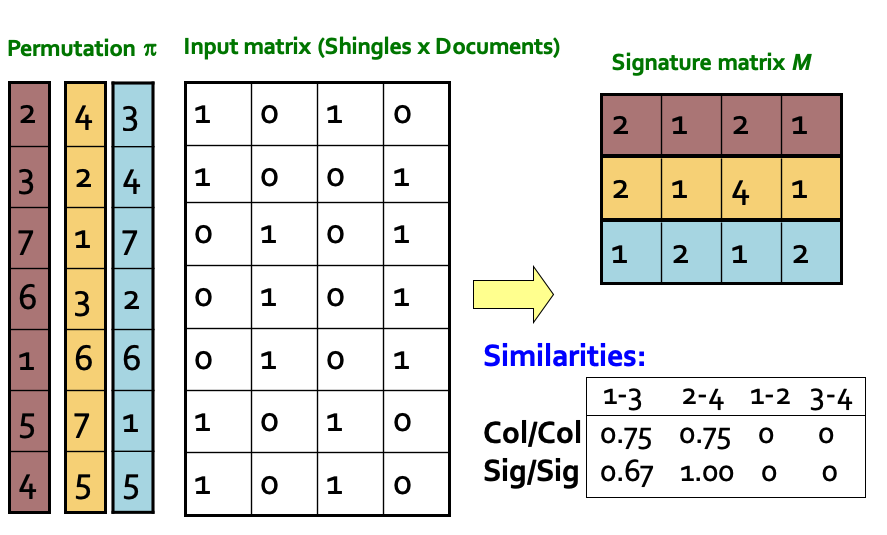
• 对于上一步得到的矩阵，随机选择一种行的排列方式π, 对于列C, h_π(C)=”C在π的排列方式下1所在的最小行号”
• 所有这样的h_π函数都称为min-hash
• 两列的min-hash值相等的概率等同于两列的jaccard相似度
• Pr[h_π(C)=h_π(C)] = Sim_jaccard(C1,C2)
• 证明：
  • 经过π重新排列，C1,C2在某一行i的取值有如下四种情况
    a. C1_i = 0, C2_i = 0
    b. C1_i = 1, C2_i = 0
    c. C1_i = 0, C2_i = 1
    d. C1_i = 1, C2_i = 1
  • 考虑C1或者C2的值为1的最小行r, r属于(b,c,d)三种情况之一
  • 其中r属于情况d的时候h_π(C)=h_π(C)
  • 因此Pr[h_π(C)=h_π(C)] = |d|/|b|+|c|+|d| = Sim_jaccard(C1,C2)
• 由于Pr[h_π(C)=h_π(C)] = Sim_jaccard(C1,C2)，h_π是一个局部敏感hash
• 下图展示了三个不同π排列方式下，minhash的取值
  

优化S-Curve

• 对于一个局部敏感哈希函数h，我们可以画出Pr[h_π(C)=h_π(C)] 随着Sim(C1,C2)变化得到的曲线S-Curve （注意这里的Sim不一定是jaccard相似度）

• 

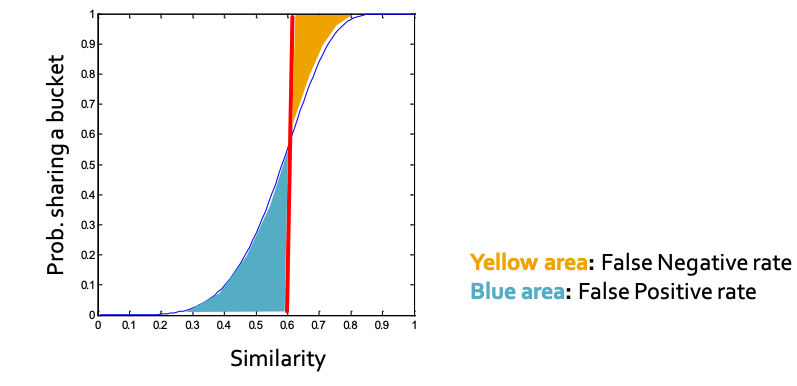
  • 如图所示，我们希望 Pr[h_π(C)=h_π(C)] 和 Sim(C1,C2)是正相关的
  • 给定一个相似度阈值s(图中红线)
  • 黄色的区域是FN:False-Negative(相似，但是hash值不等)
  • 蓝色区域是FP:False-Positive(不相似，但是shah值相等)
    • 我们希望两块区域都越小越好。根据不同的业务场景，有时降低False-Negative重要，有时降低False-Positive重要
    • 我们可以引入F-Value(1-FN-和1-FP的调和平均)来计算S-Curve的的优劣。F-Value越大，S-Curve越好

• min-hash的S-Curve

  
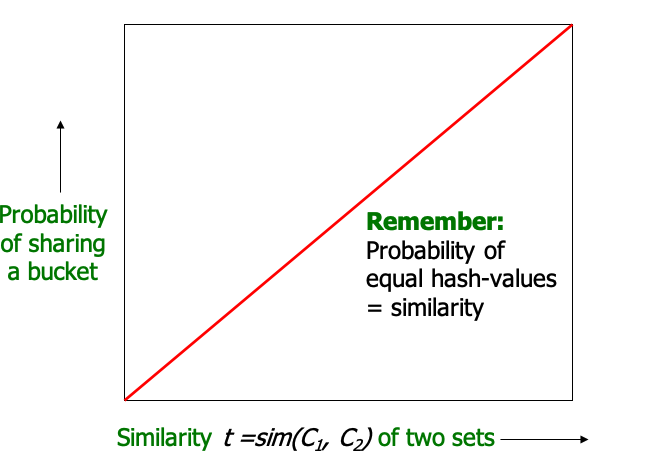
  • 显然min-hash的S-Curve不是很好（FN和FP都太大了）
  • 我们希望用一些方法让S-Curve变得更加陡峭一些

• BR优化法（我自己取得名字😂）

  • 这是一个通用的优化方法，不仅仅可以用于min-hash
  1. 随机获取M个π，用h_π作用到C上M次，将C转化为一个M维的0/1向量
  2. 将长度为M的0/1向量分为B组，每组R个数字（B*R=M）
  3. 对于C1和C2,如果他们任意一个组内的R维向量相等，认为C1和C2相似
  • B越大，FN越小，R越大FR越小
  • 试着调整 B,R的值，看看对Scurve的影响：https://www.desmos.com/calculator/lzzvfjiujn?lang=zh-CN
    • 后文我们会介绍:BR方法本质上是在组内进行AND操作，在组之间进行OR操作
    • 通过优化BR的值，我们可以获得一条在给定阈值T的情况下，FN和FP都比较小的S-Curve曲线

更详细的定义

对于LSH，我们可以给出如下更详细的定义，引入d1,d2,p1,p2四个参数：

下面列举不同距离定义下LSH函数，以及他们的参数

minhash

• 距离定义：jaccard距离
• 给定一种排列方式π，h_π(C)=”C在π的排列方式下1所在的最小行号”
• Pr[h(x) = h(y)] = 1 - d(x, y)
• (d1, d2, (1-d1), (1-d2))-sensitive

random hyperplanes hash

• 距离定义：cosine距离
• 给定一个随机向量v，h_v(x) = +1 if v·x >= 0 else -1
• Pr[h(x) = h(y)] = 1 – d(x,y) / π
• (d1, d2, (1-d1/π), (1-d2/π))-sensitive
• 详细参考stanford课件(4.lsh-theory)45页

projection hash

• 距离定义： 欧氏距离
• 给定一个向量l，将其分成n个长度为a的bucket，h_l(x) = x在l上的投影所属的bucket
• if d << a pr[h_l(x) ==h_l(x) ] >= 1-d/a
• if d >> a pr[h_l(x) ==h_l(x) ] <= 2arccos(a/d)/π
• (a/2, 2a, 1/2, 1/3)-sensitive
• 详细参考stanford课件(4.lsh-theory)51页

AND-OR 变换

• 对于单个LSH，S-Curve不够陡峭，FN和FP都太大
• 随机应用多个LSH， 得到长度为M的signature
• 将M分为B个组，每个组长度为R，B*R=M
• 组内做R次AND操作，组间等同于B次OR操作
• 通过如上操作，可以变更LSH的参数，从而陡峭化S-Curve
• (d1, d2, p1, p2)-sensitive-> (d1, d2, 1-(1-p1^R)^B, 1-(1-p2^R)^B)-sensitive

SimHash

• SimHash是谷歌2007年论文《Detecting Near-duplicates for web crawling》提出的算法，用来做文本查重。网上有很多关于SimHash具体算法介绍的文章，这里就不再赘述
• 看完哪些文章，一直知其然不知其所以然。知道看了Stanford关于LSH的课件之后，经过 深入理解simhash原理博客的点拨，才明白simhash其实也是上文框架下的一种具体文本查重解决方案。
• SimHash本质上是针对Cosine距离的一种random hyperplanes hash算法应用。下面把SimHash的步骤和本文介绍的LSH在文本去重中应用的框架对应起来
  1. 分词：shingling操作，SimHash给每个shingle增加了一个权重，这个权重只是一种优化手段，我们可以把权重都当做1，不影响对SimHash的本质理理解
  2. 将每个shingle hash成一个M维的0/1向量：本质上是生成了M个随机向量。每一列都是一个随机向量
  3. 对于每一列求和：求随机向量和文本向量的点积
  4. 计算两个文档的汉明距离，认为汉明距离小于d为相似：M个hash值分为(d+1)组，每组M/(d+1)个数，然后利用BR优化法优化S-Curve

总结

解决在海量数据（文本、图片、商品）中快速寻找相似数据的问题

1. 将数据向量化（通常得到一个高维、稀疏的向量）
2. 定义一个距离函数，以及一个阈值T，定义距离小于T为相似
3. 根据距离函数，找到一个(d1, d2, p1, p2-sensitive)的LSH函数
4. 随机选择LSH的参数，应用LSH函数M次，将向量转化为长度为M的hash值
5. 选择一组B和R的值。B*R=M， 从而得到一个(d1, d2, 1-(1-p1^r)^b, 1-(1-p2^R)^B)-sensitive 的LSH函数
6. 寻找相似数据的时候，只在最终的LSH函数值相同的分桶中找
7. 这是一个近似算法，需要权衡FN和FP。 FN的数据就被漏掉了，FP的数据可以在分桶中检查时去除，但是FP过高也会降低算法的效率

参考资料

• stanford课件(3.lsh)
• stanford课件(4.lsh-theory)
• 深入理解simhash原理